别被函数图像“绕晕”！一次搞懂函数图像里的增减、对称与极值

每次月考数学卷子发下来，总有人对着函数图像题唉声叹气。

函数图像这个知识点在高考中每年必考，但去年全国卷统计显示超过43%的考生在这类题上丢分，特别是增减趋势判断错误、对称轴找错、极值点漏算这三个坑，让多少人白白丢了关键分数。

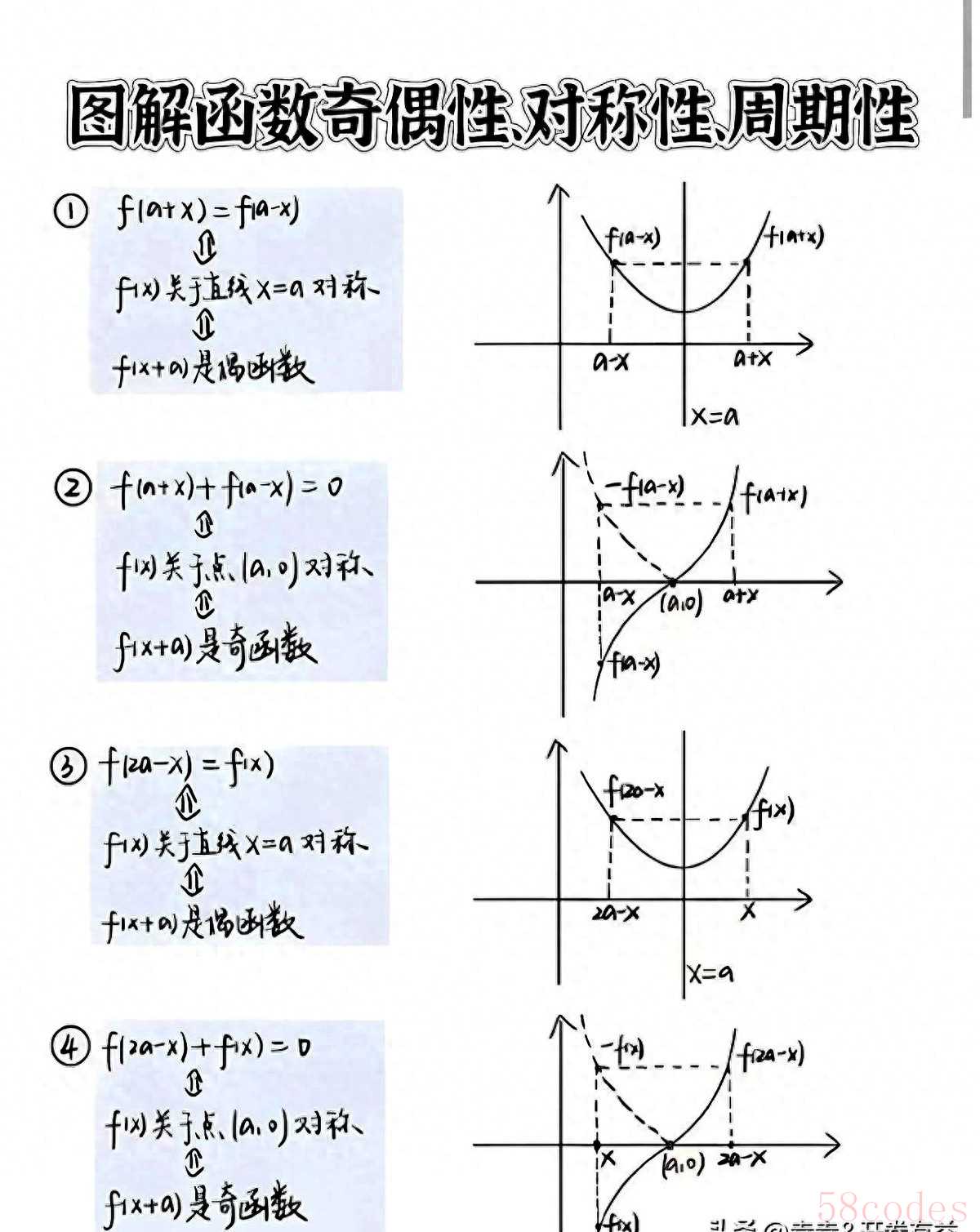
其实看穿函数图像的"微表情"，解题效率能直接翻倍。

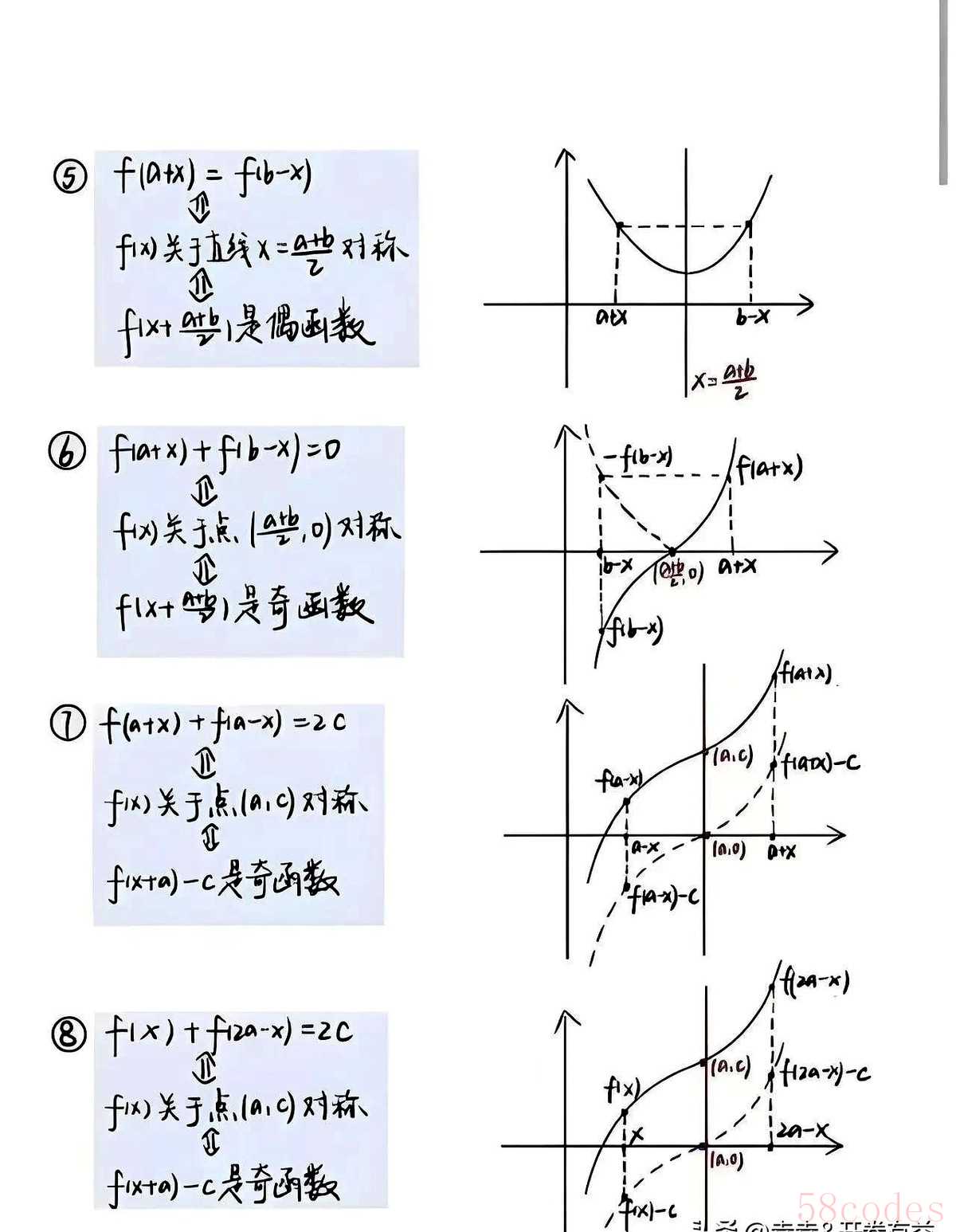
很多学生喜欢死记硬背对称公式，结果遇到三次函数y=x³+x²就直接卡壳。之前有个重点中学老师分享案例，班上有个学生每次碰到非标准抛物线就画歪对称轴，后来发现是没理解偶函数的本质是输入值的绝对值对应相同输出值。像y=2x²+4x这种函数，配方成2²-2后，对称轴x=-1的规律比硬背顶点坐标有用得多。

最近抖音上有老师用体温变化曲线类比函数增减性，播放量直接破百万。其实极值点就跟体温计的波动一样，高烧到39度再降回37度，那个39度就是局部极大值。现在很多模拟题把股票涨跌图混进函数题，学生要能看出K线图里哪个点位相当于导数为零的转折处，这种跨学科陷阱今年大概率会考。

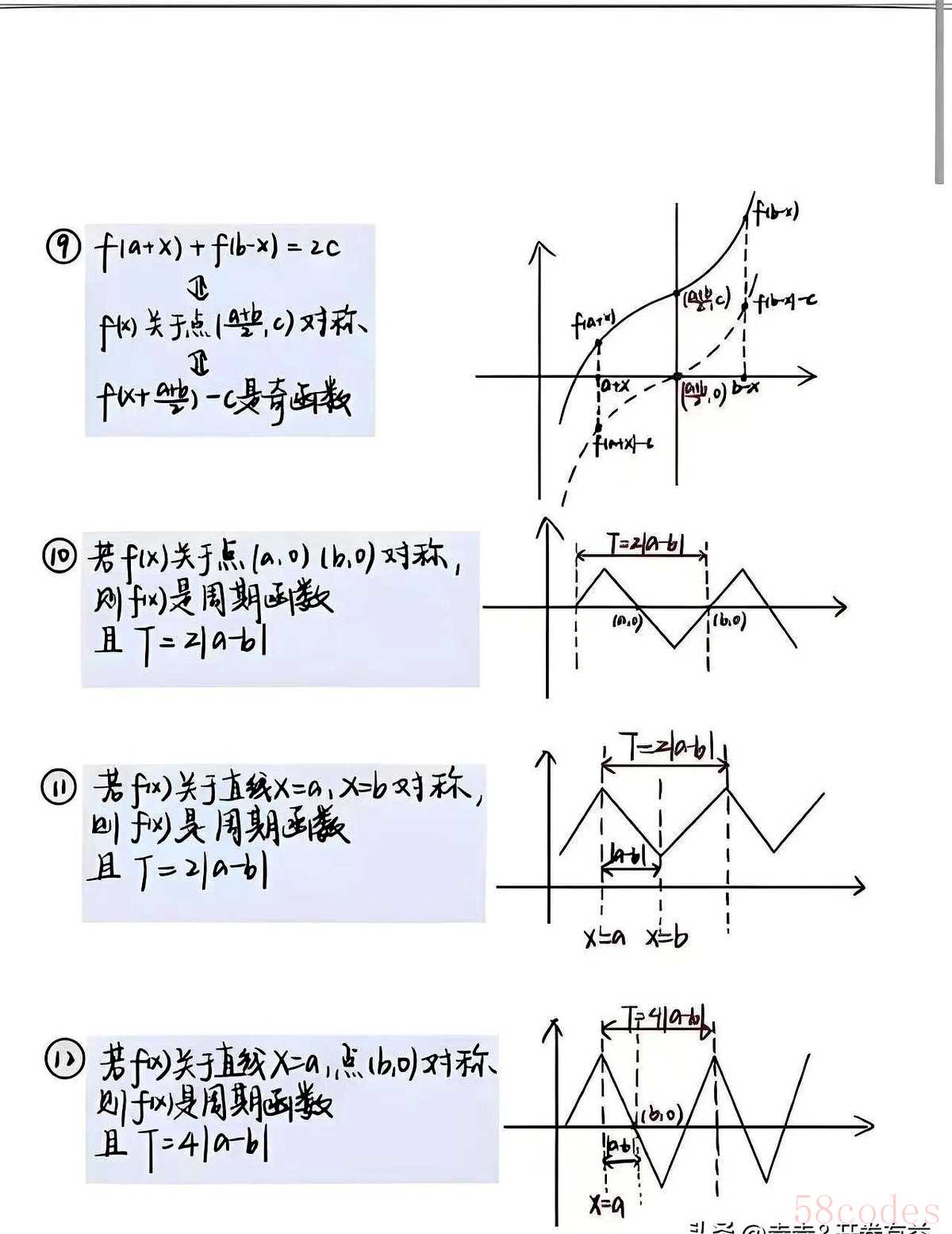
说白了函数图像就是数学里的表情包，抛物线扬起的嘴角是开口方向，波浪线的扭腰是周期变化。去年有个考生把正弦曲线对称中心标错成，后来发现记住"奇函数过原点"这个基本特征就能避免。有时候补再多的课不如盯着坐标系发会儿呆，那些起伏转折真的会自己讲故事。